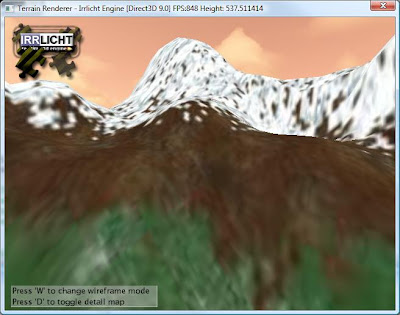
Ugh! It looks like crap. Notice how blury the texture looks. This is because there is some disruption in the texture's appearance as it is streched over the terrain. To remedy this situation we can apply a technique called texture splatting. This technique is one that is frequently used in commercial 3D games. Fortunately, PnP Terrain Creator exports the alpha maps required to implement texture splatting.
Texture Splatting
Texture splatting is a technique for texturing a terrain, using high resolution, localized tiling textures which, transition nonlinearly. You can accomplish this by blending an alpha map with each texture in your terrain. This produces unique textures tiled over the landscape, with linear alpha fades between them. This is the effect we need to avoid blurring. This approach will not only prevent bluring but it will also make the transition between textures (ie grass and dirt) look smooth.
One problem I ran into, as previously mentioned, is that Irrlicht only supports 4 textures per terrain block. My terrain has grass, snow, and dirt so I would need 6 textures to implement texture splatting (3 textures for the snow, dirt, and grass, and an alpha map for each texture).
Merging Alpha Maps Using Color Channels
Instead of using one texture for each alpha map, I could use one image and insert each grey scale alpha map into a different RGB channel. This means one texture could store 3 gray scale images. A nice side benefit is that I also save a significant amount of texture memory using this approach.

I can now represent the textures for my terrain using four textures instead of six. I will use three textures for the snow, dirt, and grass and a different RGB channel in one texture for each alpha map. Now that we have the textures set up we need to apply them to the terrain. We could do this in hardware using the fixed function pipeline. However, the fixed function pipeline does not allow for the explicit reading of individual texture color channels in hardware, therefore combined alpha maps would not be possible using the fixed function pipeline and each terrain texture would require it’s own alpha map in texture memory. This means texture splatting must be implemented using a pixel shader.
Texture Splatting With Pixel Shaders
For both HLSL and assembly implementations the general approach is as follows:
- Procedurally generate a set of alpha maps for the desired terrain textures (or load pre-generated alpha maps from disk).
- Load the set of terrain textures that will be applied into memory.
- Initialize the pixel shader.
- Set the terrain texture stages for the pixel shader to reference the alpha maps and terrain textures.
- Render the geometry using the pixel shader.
- Combined Alpha Map (R= Texture1 Alpha, G=Texture2 Alpha, B=Texture 3 Alpha, A=255)
- First layered texture (alpha map stored in the red channel of Texture 1)
- Second layered texture (alpha map stored in the green channel of Texture 1)
- Third layered texture (alpha map stored in the blue channel of Texture 1)
float4x4 matViewProjection : ViewProjection;
float texScale = 10.0;
sampler AlphaMap = sampler_state
{
ADDRESSU = WRAP;
ADDRESSV = WRAP;
ADDRESSW = WRAP;
};
sampler TextureOne = sampler_state
{
MipFilter = LINEAR;
MinFilter = LINEAR;
MagFilter = LINEAR;
ADDRESSU = WRAP;
ADDRESSV = WRAP;
ADDRESSW = WRAP;
};
sampler TextureTwo = sampler_state
{
MipFilter = LINEAR;
MinFilter = LINEAR;
MagFilter = LINEAR;
ADDRESSU = WRAP;
ADDRESSV = WRAP;
ADDRESSW = WRAP;
};
sampler TextureThree = sampler_state
{
MipFilter = LINEAR;
MinFilter = LINEAR;
MagFilter = LINEAR;
ADDRESSU = WRAP;
ADDRESSV = WRAP;
ADDRESSW = WRAP;
};
struct VS_INPUT
{
float4 Position : POSITION0;
float2 alphamap : TEXCOORD0;
float2 tex : TEXCOORD1;
};
struct VS_OUTPUT
{
float4 Position : POSITION0;
float2 alphamap : TEXCOORD0;
float2 tex : TEXCOORD1;
};
struct PS_OUTPUT
{
float4 diffuse : COLOR0;
};
VS_OUTPUT vs_main( VS_INPUT Input )
{
VS_OUTPUT Output;
Output.Position = mul( Input.Position, matViewProjection );
Output.alphamap = Input.alphamap;
Output.tex = Input.tex;
return( Output );
}
PS_OUTPUT ps_main(in VS_OUTPUT input)
{
PS_OUTPUT output = (PS_OUTPUT)0;
vector a = tex2D(AlphaMap, input.alphamap);
vector i = tex2D(TextureOne, mul(input.tex, texScale));
vector j = tex2D(TextureTwo, mul(input.tex, texScale));
vector k = tex2D(TextureThree, mul(input.tex, texScale));
float4 oneminusx = 1.0 - a.x;
float4 oneminusy = 1.0 - a.y;
float4 oneminusz = 1.0 - a.z;
vector l = a.x * i + oneminusx * i;
vector m = a.y * j + oneminusy * l;
vector n = a.z * k + oneminusz * m;
output.diffuse = n;
return output;
}
technique Default_DirectX_Effect
{
pass Pass_0
{
VertexShader = compile vs_2_0 vs_main();
PixelShader = compile ps_2_0 ps_main();
}
}
Texture Splatting - Success!
At this point we have our textures set up and a pixel shader written to implement texture splatting. After writing the code to wire everything up in Irrlicht, I got this result:
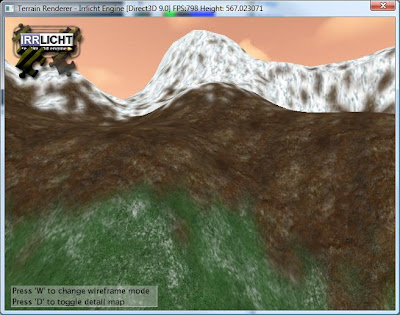
Success! Notice the difference! The textures are no longer blurred and the transition between textures is nice and smooth. Now that I have successfully implemented splatting, I need to figure out a way to seam terrain blocks togeather so that I can build massive terrains. Currently Irrlicht only supports terrain blocks of 128x128. That means you need to break up large terrains into blocks and render them appropriately. This will be my next task.

